CHAMP MAGNÉTIQUE (2).

source Wikipédia

lien historique & auteurs

Creative Commons License

Cette création est mise à disposition sous un contrat Creative Commons.

Manifestations du champ magnétique

En physique classique, les champs magnétiques sont issus de courants électriques. Au niveau microscopique, un électron en « orbite » autour d'un noyau atomique peut être vu comme une minuscule boucle de courant, générant un faible champ magnétique et se comportant comme un dipôle magnétique. Selon les propriétés des matériaux, ces structures magnétiques microscopiques vont donner lieu à essentiellement trois types de phénomènes :

Dans certains cas, les champs générés par des électrons d'atomes voisins présentent une certaine tendance à s'aligner les uns par rapport aux autres, un champ magnétique macroscopique, c'est-à-dire une aimantation spontanée, est susceptible d'apparaître. C'est le phénomène de ferromagnétisme, expliquant l'existence d'aimants permanents. Il est possible de détruire le champ magnétique d'un aimant en le chauffant au-delà d'une certaine température. L'agitation thermique générée par le chauffage brise les interactions entre atomes proches qui étaient responsables de l'alignement des champs magnétiques atomiques. En pratique, le phénomène de ferromagnétisme disparaît au-delà d'une certaine température appelée température Curie. Elle est de 770 degrés Celsius pour le fer.
En l'absence de ferromagnétisme, ou à une température trop élevée pour que celui-ci apparaisse, la présence d'un champ magnétique externe peut amener les champs microscopiques à s'aligner dans le sens du champ. Ce phénomène est appelé paramagnétisme. La transition entre l'état ferromagnétique et l'état paramagnétique se fait par l'intermédiaire d'une transition de phase dite de second ordre (c'est-à-dire que l'aimantation tend continûment vers 0 à mesure que la température approche la température de Curie, mais que sa dérivée par rapport à la température diverge à la transition). Le premier modèle mathématique permettant de reproduire un tel comportement s'appelle le modèle d'Ising, dont la résolution, considérée comme un tour de force mathématique, a été effectuée par le prix Nobel de chimie Lars Onsager en 1944.
À l'inverse, certains matériaux tendent à réagir en alignant leurs champs magnétiques microscopiques de façon antiparallèle avec le champ, c'est-à-dire s'efforçant de diminuer le champ magnétique imposé de l'extérieur. Un tel phénomène est appelé diamagnétisme.

Courants électriques

Tout courant électrique génère un champ magnétique, ce qu'a montré l'expérience historique d'Ørsted.

La présence d'un courant permet donc d'influencer localement le champ magnétique, c'est le principe des électroaimants. Ce champ magnétique est d'autant plus intense que le courant l'est. Réciproquement, un champ magnétique variable est susceptible de générer un courant électrique. C'est le principe de l'induction magnétique qu'utilisent toutes les machines électriques.

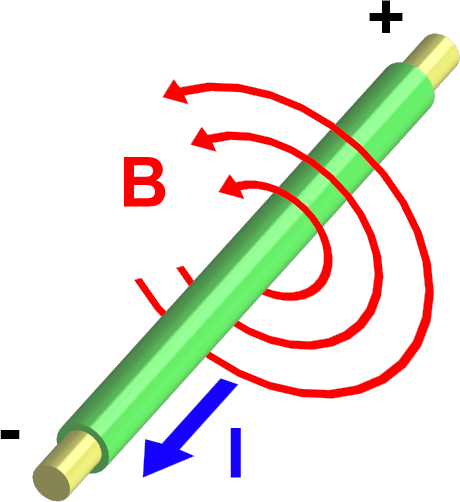
Un courant électrique , d'intensité I (I > 0), parcourant un fil crée un champ magnétique B autour de celui-ci.

Champs magnétiques des planètes

La Terre, comme la plupart des planètes du système solaire, possède un champ magnétique. Ce champ magnétique terrestre — qui protège la Terre en déviant les particules chargées issues du Soleil dans une région appelée magnétosphère — est principalement d'origine interne. On suppose qu'il est issu d'effets de convection de la matière située dans le noyau interne de la Terre, principalement composé de fer et de nickel liquide. En particulier, des courants (bien que très faibles), parcourant le noyau induiraient ce champ magnétique, par un processus appelé effet dynamo.

La valeur moyenne du champ magnétique terrestre est d'environ 0,5 gauss (soit 5×10^-5 T). Le champ magnétique terrestre fluctue au cours du temps : sa direction et son intensité ne sont pas constantes. De plus, il n'est pas homogène en tout point du globe.

Représentation d'artiste du champ magnétique terrestre.

En particulier, les champs magnétiques des planètes Jupiter et Saturne, les plus intenses après celui du Soleil sont actuellement beaucoup étudiés afin notamment de comprendre le décalage entre l'orientation du champ magnétique et l'axe de rotation de la planète, ainsi que ses variations. La mesure du champ magnétique de Saturne est l'un des objectifs de la mission Cassini-Huygens, tandis que celui de Jupiter sera étudié par la sonde JUNO. L'origine de ces champs est supposée liée aux mouvements du noyau d'hydrogène métallique qu'elles abritent.

Au niveau des pôles magnétiques de ces planètes, le champ a tendance à guider les particules chargées, issues par exemple du vent solaire. Celles-ci, très énergétiques, interagissent parfois avec l'atmosphère de la planète : c'est ce que l'on peut observer sous la forme des aurores polaires.

Aurores au pôle de Jupiter .

Monopôles magnétiques

Une des différences fondamentales entre le champ électrique et le champ magnétique est que l'on observe dans la nature des particules possédant une charge électrique, alors que l'on n'observe ni particule ni objet possédant une charge magnétique. En pratique cela se traduit par l'absence de configurations possédant un champ magnétique purement radial, ce qui mathématiquement correspond au fait que le champ magnétique est de divergence nulle.

En particulier, tout aimant possède un pôle nord et un pôle sud magnétique. Si l'on casse cet aimant en deux, on se retrouve avec deux aimants ayant chacun un pôle nord et un pôle sud magnétique. Mathématiquement, cette propriété se traduit par le fait que la divergence du champ magnétique est nulle, propriété formalisée par l'une des équations de Maxwell. Des objets hypothétiques ne possédant qu'un seul pôle magnétique sont appelés monopôles magnétiques.

L'existence de monopôles magnétiques n'a pour l'heure pas été prouvée. D'un point de vue physique, rien n'interdit cependant leur existence. Dans cette hypothèse, l'électrodynamique quantique prédit certaines de leurs propriétés, à savoir que la charge électrique et la charge magnétique sont deux entités nécessairement discrètes, dont le produit de la plus petit valeur positive est égale au produit d'un nombre entier par la constante de Planck réduite. On parle dans ce cas de monopôles de Dirac, nommés en l'honneur du physicien anglais Paul Dirac qui a prouvé cette propriété de discrétisation.

Dans la théorie de Yang-Mills, on fait intervenir un monopôle de 't Hooft-Polyakov.

Origine relativiste

En 1905, Albert Einstein montra comment le champ magnétique apparaît, comme un des aspects relativistes du champ électrique, plus précisément dans le cadre de la relativité restreinte.

Il se présente comme le résultat de la transformation lorentzienne d'un champ électrique d'un premier référentiel à un second en mouvement relatif.

Lorsqu'une charge électrique se déplace, le champ électrique engendré par cette charge n'est plus perçu par un observateur au repos comme à symétrie sphérique, à cause de la dilatation du temps prédite par la relativité. On doit alors employer les transformations de Lorentz pour calculer l'effet de cette charge sur l'observateur, qui donne une composante du champ qui n'agit que sur les charges se déplaçant : ce que l'on appelle « champ magnétique ».

On peut ainsi décrire les champs magnétique et électrique comme deux aspects d'un même objet physique, représenté en théorie de la relativité restreinte par un tenseur de rang 2.

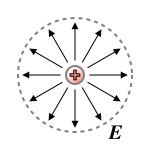
Une particule chargée, au repos dans le vide, engendre un champ électrique isotrope, identique dans toutes les directions de l'espace.

En revanche, son déplacement brise cette symétrie, à cause d'effets relativistes : cette déformation est à l'origine du champ magnétique.

Champ magnétique, excitation magnétique et aimantation

Un matériau plongé dans un champ magnétique est susceptible de générer un nouveau champ magnétique au sein de celui-ci. Plus précisément, il peut générer une densité de dipôles magnétiques suffisante pour que celle-ci génère un champ magnétique mesurable. Un tel phénomène est appelé aimantation.

Un matériau ferromagnétique possède une aimantation spontanée, c'est-à-dire existant même en l'absence de champ extérieur, mais même dans ce cas, la valeur de l'aimantation est influencée par l'intensité du champ magnétique extérieur. Le champ généré par l'aimantation s'ajoute au champ initial, et c'est la somme des deux qui est observée. Dans un tel cas, le terme de champ magnétique désigne le champ total, et le champ initial prend le nom d'excitation magnétique.

En d'autres termes, on est parfois amené à distinguer le champ initial, l'excitation magnétique, notée H, du champ total, noté B, reliés l'un à l'autre par la relation :

$\boldsymbol B = \mu_0 \left( \boldsymbol H + \boldsymbol M \right)$ ,

μ₀ étant la perméabilité magnétique du vide et M l'aimantation du milieu.

L'aimantation est une conséquence de l'excitation magnétique, et il existe donc une fonction (éventuellement compliquée)

$\boldsymbol M = \boldsymbol M \left( \boldsymbol H \right)$ .

Dans les cas les plus simples, ces deux quantités sont proportionnelles l'une de l'autre, et l'on définit la susceptibilité magnétique χ, quantité sans unité, par :

$\boldsymbol M = \chi \boldsymbol H$

ce qui permet d'écrire :

$\boldsymbol B = \mu_0 \left(1 + \chi \right) \boldsymbol H = \mu_0 \mu_r \boldsymbol H$

avec

μ_r = 1 + χ,

qui est appelé la perméabilité magnétique (ou perméabilité) du milieu.

Quand le matériau est anisotrope, la relation entre excitation et aimantation peut être plus complexe. En particulier, ces deux quantités peuvent ne pas avoir même direction. Dans ce cas, si l'on suppose qu'elles sont reliées par une relation linéaire, celle-ci est sous formematricielle.

Différence entre champ magnétique et excitation magnétique

Il est bien souvent difficile de distinguer un champ magnétique B d'une excitation magnétique H d'autant qu'ils sont souvent donnés comme étant liés par une perméabilité magnétique relativement complexe à estimer (car fonction du matériau et de la norme d'un éventuel courant électrique embrassant celui-ci).

En fait, l'induction magnétique est un champ au sens physique du terme c'est-à-dire qu'en un point de l'espace soumis à ce champ, une force d'attraction (ou de répulsion) magnétique est susceptible de s'appliquer.

Quant à l'excitation magnétique, c'est une fonction mathématique qui fait le lien entre un courant électrique et un champ magnétique. Elle est parfaitement définie par l'équation de Maxwell-Ampère :

$\boldsymbol \nabla \wedge \boldsymbol H \ = \boldsymbol j$ (formulation locale),

ou bien

$\oint_C \boldsymbol H \cdot \mathrm{d} \boldsymbol l = nI$ (formulation intégrale).

Dans l'air, les vecteurs H et B sont égaux à une constante multiplicative près (perméabilité magnétique de l'air, proche de celle du vide). On peut choisir d'étudier indifféremment l'un ou l'autre du fait de la relation rigide qui les lie. Par contre, dans un matériau quelconque, en particulier pour les matériaux ferromagnétiques, les deux vecteurs doivent être clairement distingués car en plus des différences que nous venons de voir, des phénomènes de non-linéarités (saturation magnétique et hystérésis) compliquent les relations entre B et H.

Le champ d'excitation H est parfois appelé « champ courant » pour mieux souligner son origine.

Visualisation du champ magnétique

Lignes de champ

Par définition, les lignes de champ du champ magnétique sont l'ensemble des courbes « en tout point » tangentes à B'. Albert Einstein montra comment le champ magnétique apparaît, comme un des aspects relativistes du champ électrique, plus précisément dans le cadre de larelativité restreinte.

Ces lignes relient les pôles magnétiques, et par convention on les oriente de sorte que les lignes de champ d'un aimant entrent par le sud et ressortent par le nord. Leur expression locale est telle que :

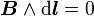$\boldsymbol B \wedge {\mathrm d} \boldsymbol l = 0$ .

où dl, de coordonnées (dx, dy, dz), est un vecteur infinitésimal. Une équation paramétrique décrivant les lignes de champ se déduit de la formule ci-dessus en choisissant une variable d'intégration (par exemple x si la composante B_x est non nulle) et en intégrant les équations, qui en coordonnées cartésiennes donnent

$\frac{{\mathrm d} y}{{\mathrm d} x} = \frac{B_y}{B_x}$ ,

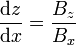
$\frac{{\mathrm d} z}{{\mathrm d} x} = \frac{B_z}{B_x}$

Mise en évidence de lignes de champ magnétique par des brindilles d'acier et de la limaille.